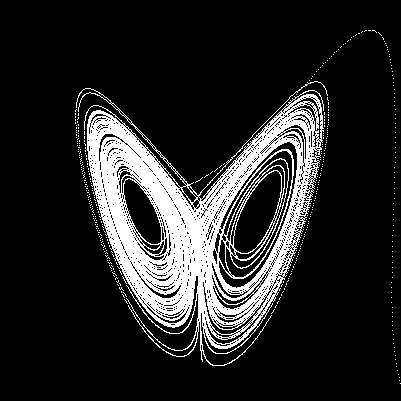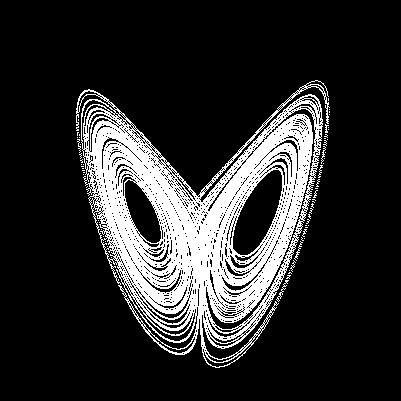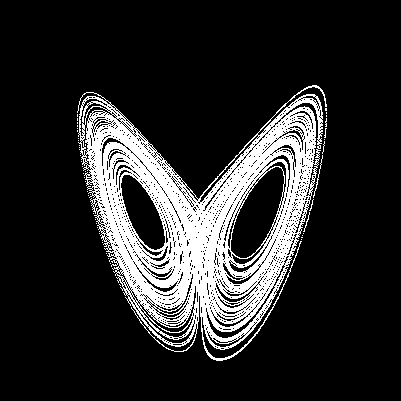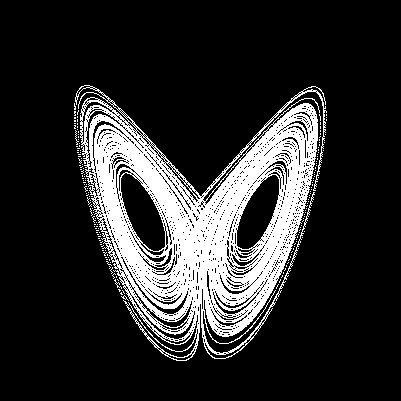Lorenz Attractors
The Lorenz Attractor is a fascinating mathematical construct that emerges from the Lorenz system, a set of differential equations first studied by meteorologist and mathematician Edward Lorenz in the 1960s. Lorenz derived these equations as a simplified model of atmospheric convection, aiming to understand the complex and often unpredictable nature of weather systems.
The Lorenz system exhibits a remarkable property known as chaotic behavior. In a chaotic system, minuscule differences in initial conditions can lead to drastically divergent outcomes over time. This extreme sensitivity makes long-term prediction practically impossible, as even the tiniest uncertainties or measurement errors will be amplified exponentially.
Lorenz's work gave rise to the evocative term "butterfly effect," suggesting that the flap of a butterfly's wings could theoretically influence the formation of a distant tornado weeks later. While this poetic description is an oversimplification, it effectively captures the essence of chaos theory - that small perturbations can have far-reaching and unpredictable consequences in complex, nonlinear systems.
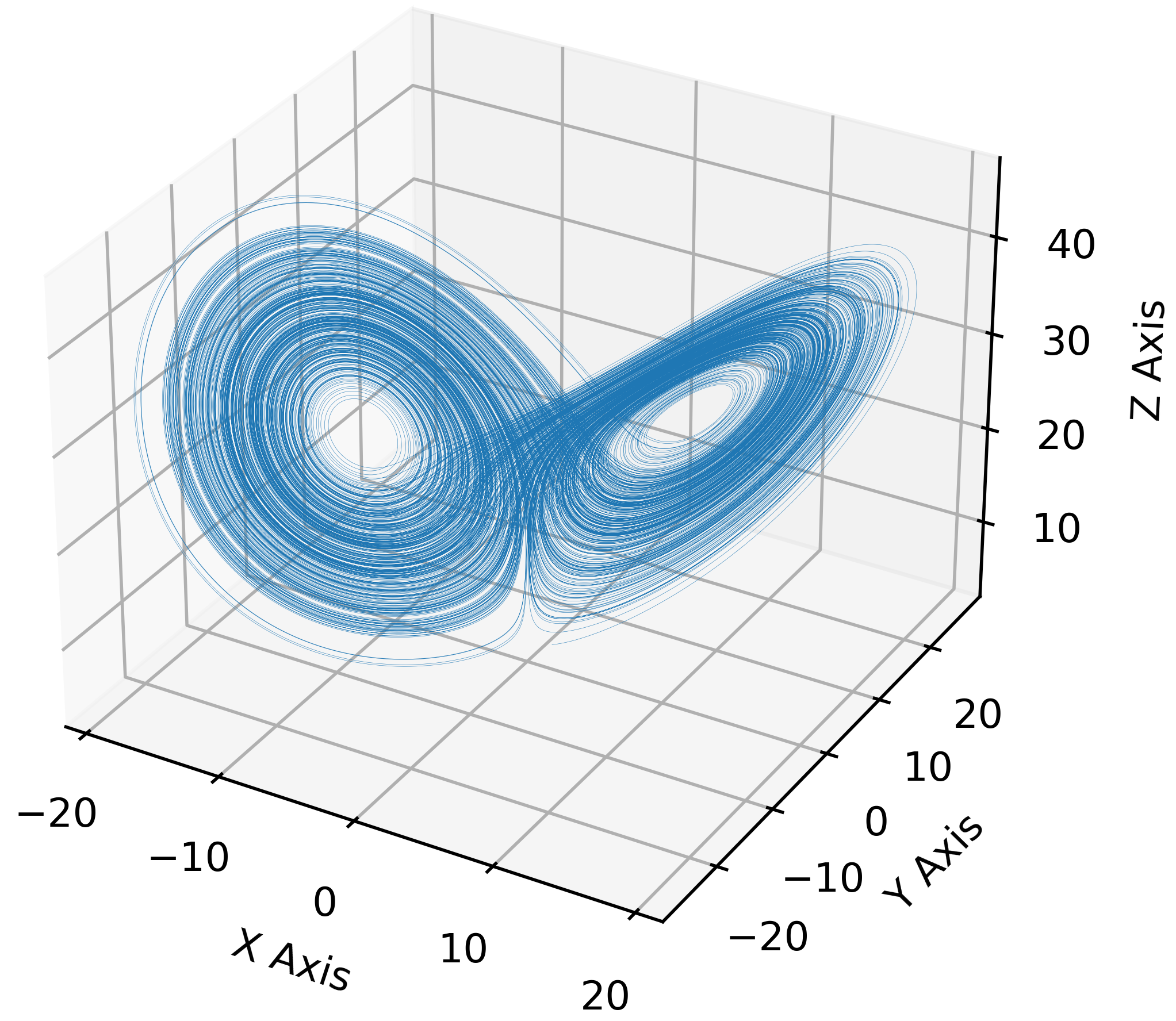
The Lorenz Attractor itself is a beautiful and intricate structure that visualizes the possible long-term behaviors of the Lorenz system. When plotted in three dimensions, the attractor resembles a pair of butterfly wings, with trajectories spiraling around two distinct lobes without ever settling into a stable state. This strange attractor has become an iconic image of chaos theory.
Beyond its aesthetic appeal, the Lorenz Attractor has had a profound impact on our understanding of complex systems across various disciplines, from meteorology and physics to biology and economics. It demonstrates that even simple deterministic equations can give rise to highly complex, chaotic behavior. The study of chaos has led to significant advancements in fields such as turbulence, population dynamics, and even heart rhythms.